1091. 二进制矩阵中的最短路径

2020-05-17

LeetCode

BFS, 搜索

5 分钟读完 (大约 694 个字) 0次访问

leetcode 1091. 二进制矩阵中的最短路径

题目：1091. 二进制矩阵中的最短路径

在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。

一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, …, C_k 组成：

相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）
C_1 位于 (0, 0)（即，值为 grid[0][0]）
C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）
如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）

返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

示例1:

输入：[[0,1],[1,0]]

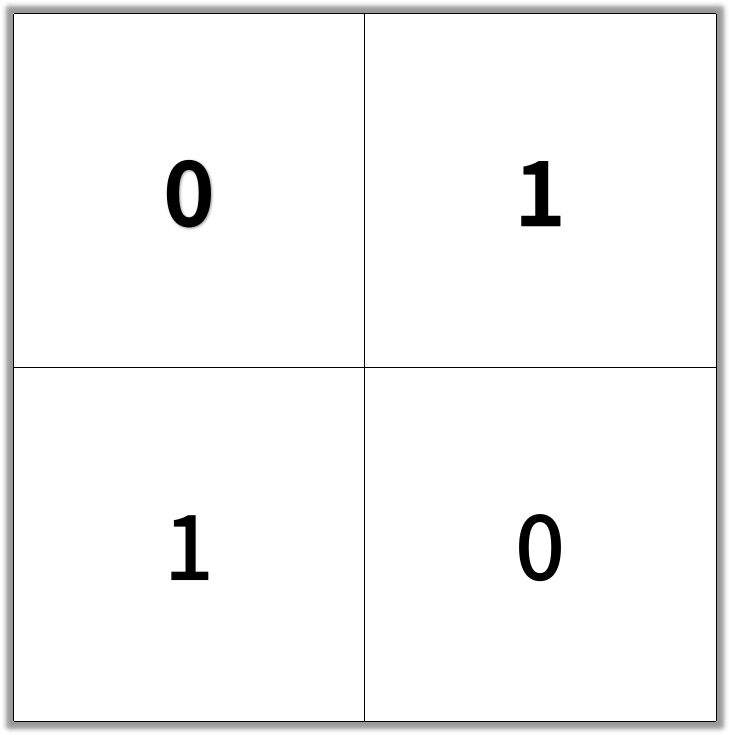
输出：2

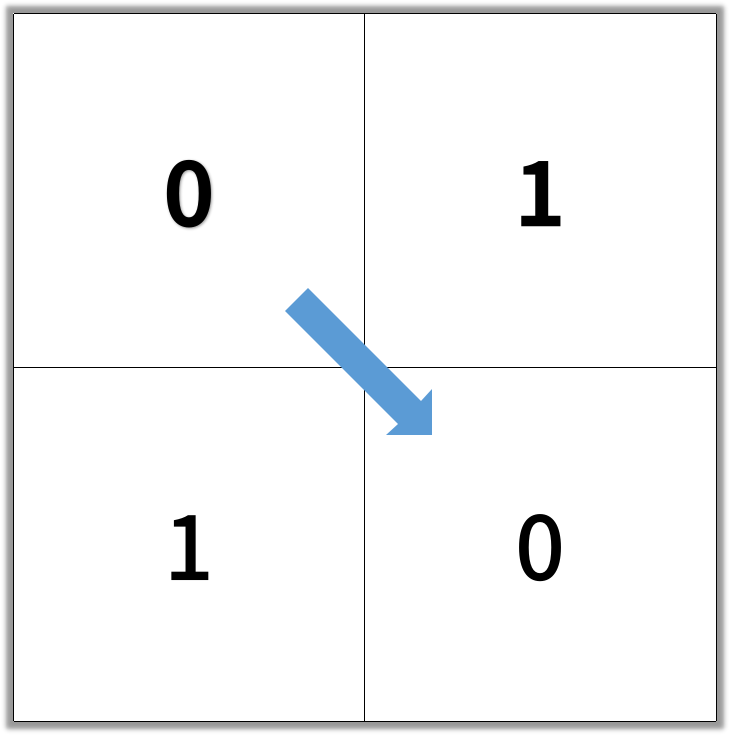
示例2:

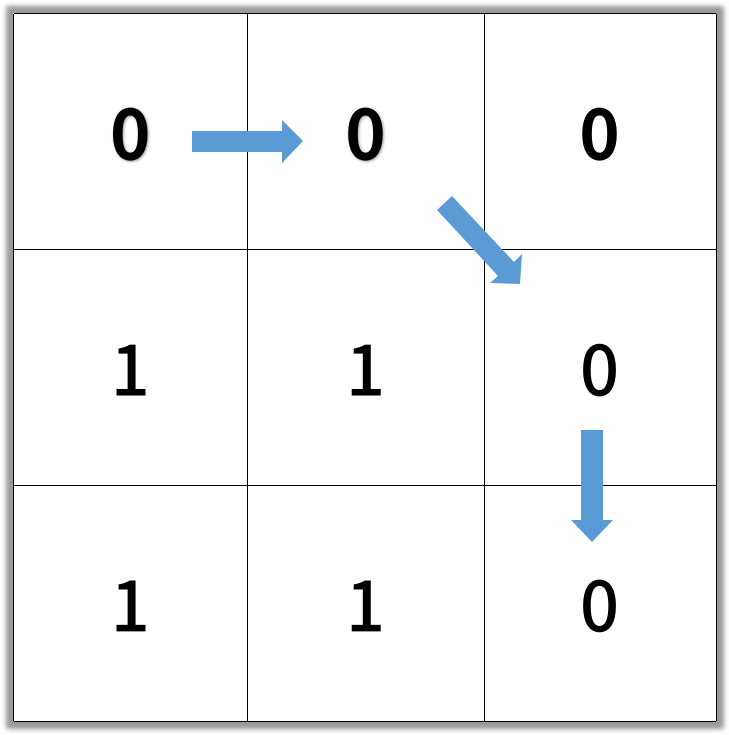
输入：[[0,0,0],[1,1,0],[1,1,0]]

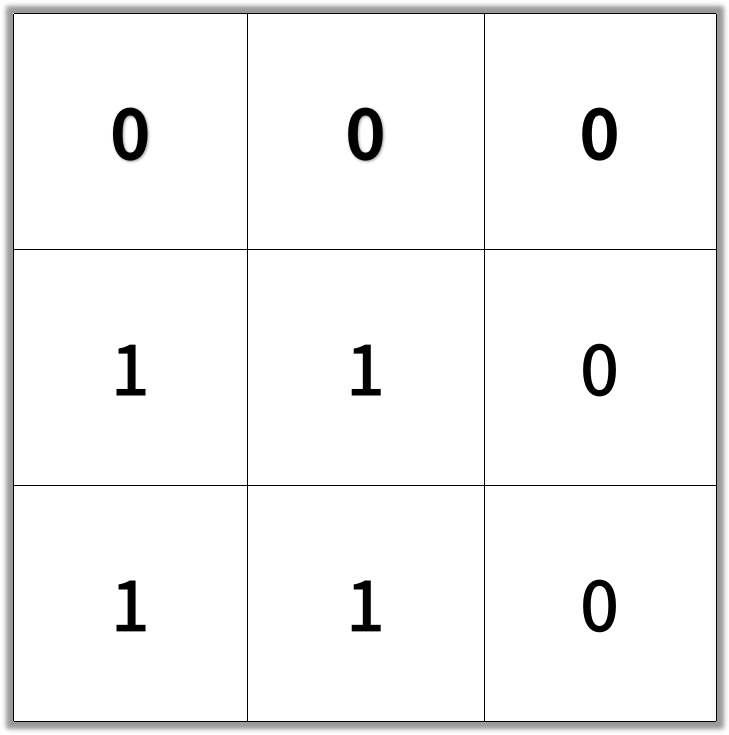
输出：4

提示:

1 <= grid.length == grid[0].length <= 100
grid[i][j] 为 0 或 1

方法：BFS（广度优先搜索）

思路：BFS（广度优先搜索），最先搜索到终点的路径长度，即为最短路径长度。

运行数据：执行用时：15 ms，内存消耗：41.4 MB

// LeetCode指定调用方法
public int shortestPathBinaryMatrix(int[][] grid) {
    	
    // 记录网格的行、列长度
    int row = grid.length;
    int col = grid[0].length;

    // 如果起点或者终点阻塞，则永远到不了终点，直接返回-1
    if(grid[0][0] == 1 || grid[row - 1][col - 1] == 1) {
        return -1;
    }

    // 如果起点即为终点，且该点不阻塞则直接返回1
    if (row - 1 == 0 && col - 1 == 0) {
        return 1;
    }

    // 可以移动的八个方向
    int[][] directions = {{0,1}, {0, -1}, {1, -1}, {1, 0}, {1, 1}, {-1, -1}, {-1, 0}, {-1, 1}};

    // 用于BFS的队列
    Queue<int[]> queue = new LinkedList<>();

    // 将起点入队
    queue.offer(new int[]{0,0});

    // 标记当前长度
    grid[0][0] = 1;

    // 记录当前队列的长度，当队列为空时，BFS全部搜索结束（用以代替 queue.isEmpty() 增加每次循环判断时的效率）
    int queueLen = 1;
    while(queueLen-- != 0){

        // 将队列中第一个位置出队
        int[] position = queue.poll();

        // 记录到前位置的路径长度
        int preLen = grid[position[0]][position[1]];

        // 遍历八个方向，向八个方向扩展
        for(int i = 0; i < 8; i++){

            // 记录扩展位置
            int currentRow = position[0] + directions[i][0];
            int currentCol = position[1] + directions[i][1];

            // 判断能否向这个方向扩展
            if(currentRow >= 0 && currentRow < row && currentCol >= 0 && currentCol < col && grid[currentRow][currentCol] == 0){

                // 标记到扩展位置的路径长度
                grid[currentRow][currentCol] = preLen + 1;

                // 判断是否已到达终点
                if (currentRow == row - 1 && currentCol == col - 1) {
                    return grid[row - 1][col - 1];
                }

                // 将扩展位置入队
                queue.offer(new int[]{currentRow, currentCol});

                // 更新当前队列长度
                queueLen++;
            }
        }
    }

    return -1;
}