leetcode 51. N 皇后
题目:51. N 皇后
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
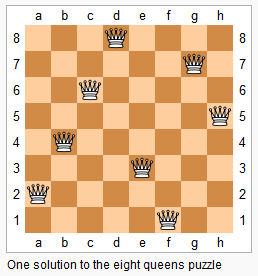
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例:
输入:4
输出:
[
[“.Q..”, // 解法 1
“…Q”,
“Q…”,
“..Q.”],
[“..Q.”, // 解法 2
“Q…”,
“…Q”,
“.Q..”]
]
解释: 4 皇后问题存在两个不同的解法。
提示:
- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
方法:Backtracking(回溯)
思路:Backtracking(回溯),将问题转化为为每一行的合适列放入一个皇后,通过三个集合columns、diagonals1、diagonals2分别记录已有皇后的所在的列数、所在从左上角指向右下角斜线位置的行数与列数的差、所在从左下角指向右上角斜线位置的行数与列数的和,用于皇后放置前的位置判断。
运行数据:执行用时:5 ms,内存消耗:39.5 MB
复杂度分析:
- 时间复杂度:O(n!),其中 n 是皇后数量。
- 空间复杂度:O(n * n),其中 n 是棋盘的行列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
public List<List<String>> solveNQueens(int n) {
List<List<String>> result = new ArrayList<List<String>>();
char[][] grid = new char[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
grid[i][j] = '.';
}
}
backtracking(result, grid, n, 0);
return result;
}
private Set<Integer> columns = new HashSet<Integer>();
private Set<Integer> diagonals1 = new HashSet<Integer>();
private Set<Integer> diagonals2 = new HashSet<Integer>();
private void backtracking(List<List<String>> result, char[][] grid, int n, int k) {
if (n == k) {
List<String> tempList = new ArrayList<>();
for (int i = 0; i < n; i++) {
tempList.add(String.valueOf(grid[i]));
}
result.add(tempList);
return ;
}
for (int i = 0; i < n; i++) {
if (columns.contains(i) || diagonals1.contains(k - i) || diagonals2.contains(k + i)) {
continue;
}
grid[k][i] = 'Q';
columns.add(i);
diagonals1.add(k - i);
diagonals2.add(k + i);
backtracking(result, grid, n, k + 1);
grid[k][i] = '.';
columns.remove(i);
diagonals1.remove(k - i);
diagonals2.remove(k + i);
}
}
|
学习所得,资料、图片部分来源于网络,如有侵权,请联系本人删除。
才疏学浅,若有错误或不当之处,可批评指正,还请见谅!



