leetcode 104. 二叉树的最大深度
题目:104. 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例1:
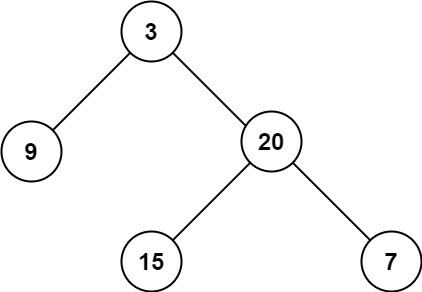
输入:root = [3,9,20,null,null,15,7]
输出:3
示例2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在 [0, 10^4] 区间内。
- -100 <= Node.val <= 100
方法一:DFS
思路:如果我们知道了左子树和右子树的最大深度 l和 r,那么该二叉树的最大深度即为 max(l,r) + 1
运行数据:执行用时:0 ms,内存消耗:41.39 MB
复杂度分析:
- 时间复杂度:O(n),其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。
- 空间复杂度:O(h),其中 h 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
1
2
3
4
5
6
7
|
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
|
方法二:DFS(非递归)
思路:如果我们知道了左子树和右子树的最大深度 l和 r,那么该二叉树的最大深度即为 max(l,r) + 1
运行数据:执行用时:5 ms,内存消耗:42.14 MB
复杂度分析:
- 时间复杂度:O(n),其中 n 为二叉树节点的个数。
- 空间复杂度:O(h),其中 h 表示二叉树的高度。实现非递归的DFS需要使用栈,栈中的元素个数不会超过二叉树的高度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int maxDepth = 1;
Stack<TreeNode> stack = new Stack<>();
Set<TreeNode> set = new HashSet<>();
stack.push(root);
set.add(root);
while (!stack.isEmpty()) {
TreeNode currTreeNode = stack.peek();
if (currTreeNode.left != null && !set.contains(currTreeNode.left)) {
stack.push(currTreeNode.left);
set.add(currTreeNode.left);
continue;
}
if (currTreeNode.right != null && !set.contains(currTreeNode.right)) {
stack.push(currTreeNode.right);
set.add(currTreeNode.right);
continue;
}
maxDepth = Math.max(maxDepth, stack.size());
stack.pop();
}
return maxDepth;
}
|
方法三:BFS
思路:BFS的层数即为二叉树的最大深度
运行数据:执行用时:1 ms,内存消耗:41.85 MB
复杂度分析:
- 时间复杂度:O(n),其中 n 为二叉树节点的个数。
- 空间复杂度:O(t),其中 t 表示二叉树同一层节点最多的那一层节点数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int maxDepth = 0;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
while (size-- > 0) {
TreeNode currTreeNode = queue.poll();
if (currTreeNode.left != null) {
queue.offer(currTreeNode.left);
}
if (currTreeNode.right != null) {
queue.offer(currTreeNode.right);
}
}
maxDepth++;
}
return maxDepth;
}
|
学习所得,资料、图片部分来源于网络,如有侵权,请联系本人删除。
才疏学浅,若有错误或不当之处,可批评指正,还请见谅!



